Princip šifrování

Z MiS
(Rozdíly mezi verzemi)
Přejít na: navigace, hledání
(→Šifrování asymetrickou šifrovací metodou: Doplnění obrázků)
(→Běžné využití: TLS místo SSL.)
 
(Není zobrazeno 13 mezilehlých verzí od 1 uživatele.)
Řádka 1: Řádka 1:
−
[[Category:VSE]][[Category:Sítě]][[Category:Informatika]][[Category:Bezpečnost]][[Category:CRI]]
+
[[Category:VSE]][[Category:Sítě]][[Category:Informatika]][[Category:Bezpečnost]][[Category:CRI]][[Category:Stránky s obrázky]][[Category:Šifrování a podpis]]
 +
 
 +
<div class="Poznamka">
 +
Nepleťte ''kódování'' s&nbsp;''šifrováním''!!!
 +
 
 +
Viz také: [[K%C3%B3dov%C3%A1n%C3%AD-%C5%A1ifrov%C3%A1n%C3%AD-hashov%C3%A1n%C3%AD]]
 +
</div>
 +
 
 +
 
  
 
== Rozdělení šifrovacích metod ==
 
== Rozdělení šifrovacích metod ==
Řádka 11: Řádka 19:
 
** soukromý klíč: zná pouze vlastník
 
** soukromý klíč: zná pouze vlastník
 
** veřejný klíč: smí znát kdokoli
 
** veřejný klíč: smí znát kdokoli
−
* Postupným použitím soukromého i veřejného klíče dostaneme původní zprávu.
 
 
* Zpráva zašifrovaná veřejným klíčem lze dešifrovat pouze soukromým klíčem a naopak.
 
* Zpráva zašifrovaná veřejným klíčem lze dešifrovat pouze soukromým klíčem a naopak.
 +
 +
 +
 +
== Porovnání vlastností ==
 +
; Asymetrické šifrovací metody
 +
# Dokáží zajistit nepopiratelnost odeslání zprávy.
 +
#: Autor zprávy nemůže popřít její odeslání.
 +
# Ulehčují problém s&nbsp;bezpečným předáním klíče potenciálně nebezpečnou sítí.
 +
#: Nevadí odposlechnutí klíče třetí osobou, je jen třeba zabránit podvržení falešného klíče.
 +
# Jedna kombinace veřejného a soukromého klíče stačí pro komunikaci s libovolným počtem partnerů.
 +
# Každý účastník zodpovídá za svůj soukromý klíč, není zde sdílená zodpovědnost za vyzrazení klíče.
 +
 +
; Symetrické šifrovací metody
 +
# Jsou výpočetně méně náročné.
  
  
Řádka 26: Řádka 47:
  
 
[[Soubor:sifr01-1_vice.png]]
 
[[Soubor:sifr01-1_vice.png]]
 +
 +
  
 
== Šifrování asymetrickou šifrovací metodou ==
 
== Šifrování asymetrickou šifrovací metodou ==
 
* Každý účastník komunikace má pár veřejný + soukromý klíč.
 
* Každý účastník komunikace má pár veřejný + soukromý klíč.
 +
* Pokud zprávu zašifrujeme soukromým klíčem účastníka, rozšifrovat lze '''pouze''' veřejným klíčem téhož účastníka. A naopak co zašifrujeme veřejným klíčem, lze rozšifrovat '''pouze''' soukromým.
 
* Odesilatel si nechává svůj soukromý klíč, ten nikomu nesděluje.
 
* Odesilatel si nechává svůj soukromý klíč, ten nikomu nesděluje.
 
* Veřejný klíč může znát kdokoli, případné přečtení při předávání veřejnou sítí tedy není rizikem.
 
* Veřejný klíč může znát kdokoli, případné přečtení při předávání veřejnou sítí tedy není rizikem.
 +
 +
[[Soubor:sifr_klice-ver-soukr.png]]
 +
 +
=== Zabezpečení proti přečtení zprávy ===
 +
* K&nbsp; zabezpečení zprávy proti přečtení by stačilo, kdyby odesilatel zprávu šifroval příjemcovým veřejným klíčem.
 +
* Taková zpráva lze poté rozšifrovat pouze příjemcovým soukromým klíčem, který zná pouze příjemce.
 +
* Odesilatel by teoreticky nemusel mít dvojici klíčů vůbec vygenerovanou.
  
 
[[Soubor:sifr02_asym.png]]
 
[[Soubor:sifr02_asym.png]]
 +
 +
=== Zabezpečení proti přečtení zprávy '''a zároveň''' proti podvržení falešné zprávy ===
 +
* V&nbsp;předchozím případě sice útočník nemůže zprávu přečíst, může ale zajistit, aby příjemce zprávu neobdržel (zničit zprávu) a&nbsp;poslat příjemci falešnou zprávu.
 +
* Asymetrické šifrovací metody však nabízí zabezpečení i proti tomuto způsobu útoku.
 +
* Odesilatel může zprávu zašifrovat příjemcovým veřejným klíčem '''a&nbsp;navíc i&nbsp;'''svým soukromým. Takovou zprávu útočník nemůže zfalšovat, protože by musel znát odesilatelův soukromý klíč.
 +
* Příjemce pak zprávu dešifruje odesilatelovým veřejným klíčem a&nbsp;svým soukromým.
  
 
[[Soubor:sifr02-1_vice.png]]
 
[[Soubor:sifr02-1_vice.png]]
 +
 +
=== Lze na takovou komunikaci vůbec zaútočit? ===
 +
* Pokud si uživatel a&nbsp;příjemce vyměnili své veřejné klíče spolehlivou cestou (například si je předali osobně), pak je role útočníka velmi obtížná.
 +
* Zbývá mu hledat chyby v&nbsp;šifrovacích programech nebo útočit tzv. hrubou silou (zkoušet uhodnout klíč). Pravděpodobnost takového útoku by měla být malá.
 +
* Problematická je situace, kdy si odesilatel a&nbsp;příjemce potřebují vyměnit své veřejné klíče pomocí nezabezpečené sítě. V&nbsp;tu chvíli může útočník oběma podsunout svůj veřejný klíč a&nbsp;poté se pokusit o&nbsp;útok man-in-the-middle.
 +
* V&nbsp;praxi se proto pro předávání klíčů používají [[Certifikační autorita|certifikační autority]].
 +
<div class="Poznamka">Všimněte si, že nám nevadí, když si útočník veřejné klíče přečte. Soukromé klíče, které musí zůstat tajné, se nikam nepředávají. To je veliká výhoda proti symetrickým šifrovacím metodám!</div>
 +
 +
  
 
== Běžné využití ==
 
== Běžné využití ==
Řádka 40: Řádka 86:
 
* Šifrování většího objemu dat se obvykle následně provádí symetrickými šifrovacími metodami.
 
* Šifrování většího objemu dat se obvykle následně provádí symetrickými šifrovacími metodami.
  
−
 
+
; TLS
−
== Porovnání vlastností ==
+
* Vrstva pro šifrovanou komunikaci (implementace části prezentační vrstvy).
−
Asymetrické šifrovací metody:
+
* Typicky se používá pro šifrovaný přenos dat protokolu HTTP (https://...).
−
* zajišťují prokazatelnost odeslání dat. (Autor zprávy nemůže popřít její odeslání.)
+
* Dříve se používal jeho předchůdce SSL.
−
* Umožňují bezpečné předání klíče potenciálně nebezpečnou sítí.
+
* Viz také: [https://en.wikipedia.org/wiki/Transport_Layer_Security]
−
* Jedna kombinace veřejného a soukromého klíče stačí pro komunikaci s libovolným počtem partnerů.
+
−
 
+
−
Symetrické šifrovací metody:
+
−
* jsou výpočetně méně náročné.
+
−
* Stačí kratší délka klíče.
+
−
 
+
  
 
== Příklady šifrovacích algoritmů ==
 
== Příklady šifrovacích algoritmů ==
Řádka 82: Řádka 122:
  
  
−
== Viz také ==
+
== Zajímavost &mdash; historické šifry ==
−
* [[Rizika při práci s daty]]
+
* Césarova šifra (přelom letopočtu): [https://www.algoritmy.net/article/34/Caesarova-sifra Algoritmy.net &rarr; Caesarova šifra]
 +
** Každé písmenko zprávy posunete o&nbsp;zadaný počet písmen v abecedě.
 +
** Klíčem je zde počet písmen, o&nbsp;které posunujeme.
 +
<div class="Priklad">Příklad: <code>A h o j K a r l e</code> + klíč <code>2</code> &rarr; <code>C j q l M c t n g</code></div>
 +
* Vigenèrova šifra (1556): [https://www.algoritmy.net/article/53/Vigenerova-sifra Algoritmy.net &rarr; Vigenèrova šifra]
 +
* Šifra Playfair (1854): [http://www.shaman.cz/sifrovani/sifra-playfair.htm Shaman.cz &rarr; Šifra Playfair]
 +
* Vernamova šifra (1917): [https://cs.wikipedia.org/wiki/Vernamova_%C5%A1ifra Wikipedia.org &rarr; Vernamova šifra]
 +
** Vlastně podobný princip jako Césarova šifra, ale každé písmeno zprávy posunu o&nbsp;jiný počet znaků.
 +
** Klíčem je informace, které písmeno posunout o&nbsp;kolik znaků.
 +
** Reálně bychom brali datový soubor se zprávou a&nbsp;ke každému byte zprávy přičítali odpovídající byte z&nbsp;náhodně vygenerovaného klíče.
 +
** Je neprolomitelná, pokud dodržíme pravidla: 1) klíč stejně dlouhý jako zpráva a 2) klíč je dokonale náhodný.
 +
** Důkaz neprolomitelnosti podal Shannon v&nbsp;roce 1949.
 +
** Problém je ale s&nbsp;předáním klíče.
 +
<div class="Priklad">Příklad: <code>A h o j K a r l e</code> + klíč <code>2 3 1 4 3 2 5 4 1</code> &rarr; <code>C k p n M c w p f</code></div>
 +
* Enigma (1918)
 +
** Originální verze prolomena už ve 30. letech 20. století.
 +
** Prolomení pokročilejší verze šifry pomohlo vítězství ve 2. světové válce.
 +
** K prolomení byly používány výpočetní stroje (předchůdci počítačů), na jejich vývoji se podílel Alan Turing.
 +
 
 +
; Úkol
 +
<div class="Ukol">
 +
; Vyzkoušejte si šifru Playfair:
 +
Chcete-li vyzkoušejte si šifrování šifrou Playfair. Zkuste zakódovat text:
 +
Šifruji jako blesk!
 +
Pomocí klíče:
 +
Informatika
 +
 
 +
Řešení &mdash; výsledný šifrovaný text by měl znít:
 +
Looíl Rf, vnmg. Kmú gqbý.
 +
(Interpunkce, diakritika a velikost písmen jsou přidány náhodně.)
 +
</div>
 +
 
 +
 
 +
 
 +
== Související stránky ==
 +
* [[Rizika při práci s daty]], [[Elektronický podpis]], [[Šifrování prakticky]], [[GPG]], [[Certifikační autorita]]

Aktuální verze z 25. 3. 2021, 09:11


Nepleťte kódování s šifrováním!!!

Viz také: Kódování-šifrování-hashování


Obsah

Rozdělení šifrovacích metod

Symetrické šifrovací metody
Asymetrické šifrovací metody


Porovnání vlastností

Asymetrické šifrovací metody
  1. Dokáží zajistit nepopiratelnost odeslání zprávy.
    Autor zprávy nemůže popřít její odeslání.
  2. Ulehčují problém s bezpečným předáním klíče potenciálně nebezpečnou sítí.
    Nevadí odposlechnutí klíče třetí osobou, je jen třeba zabránit podvržení falešného klíče.
  3. Jedna kombinace veřejného a soukromého klíče stačí pro komunikaci s libovolným počtem partnerů.
  4. Každý účastník zodpovídá za svůj soukromý klíč, není zde sdílená zodpovědnost za vyzrazení klíče.
Symetrické šifrovací metody
  1. Jsou výpočetně méně náročné.


Šifrování symetrickou šifrovací metodou

Sifr01 sym.png

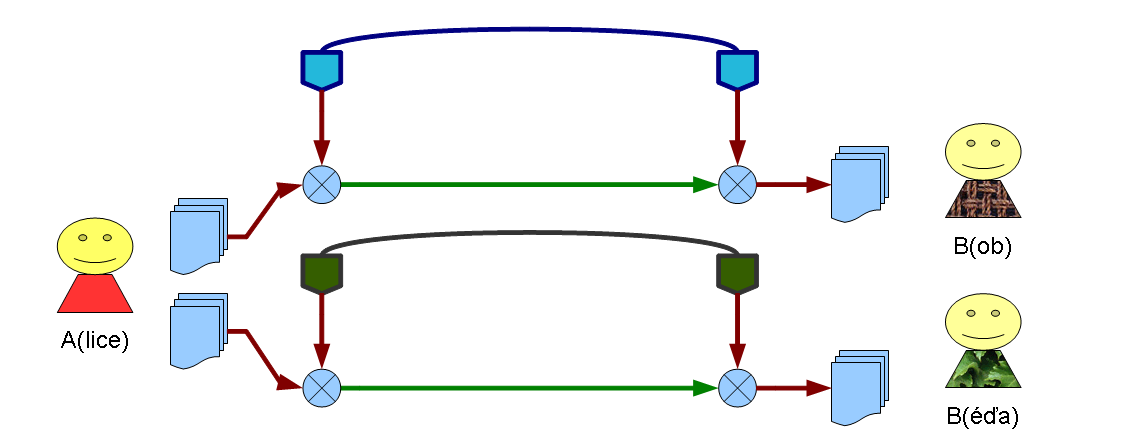
Sifr01-1 vice.png


Šifrování asymetrickou šifrovací metodou

Sifr klice-ver-soukr.png

Zabezpečení proti přečtení zprávy

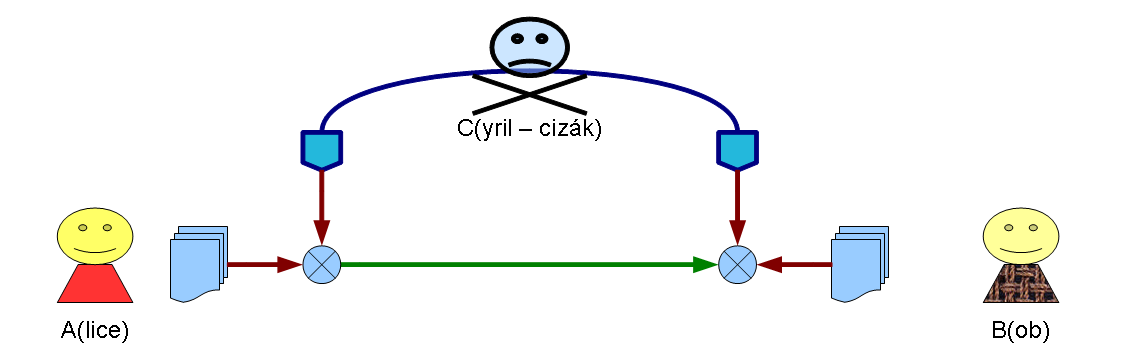
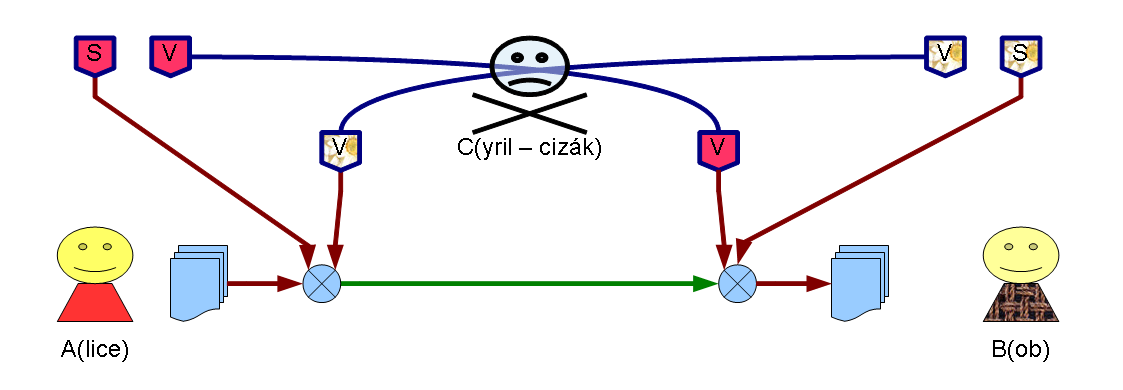
Sifr02 asym.png

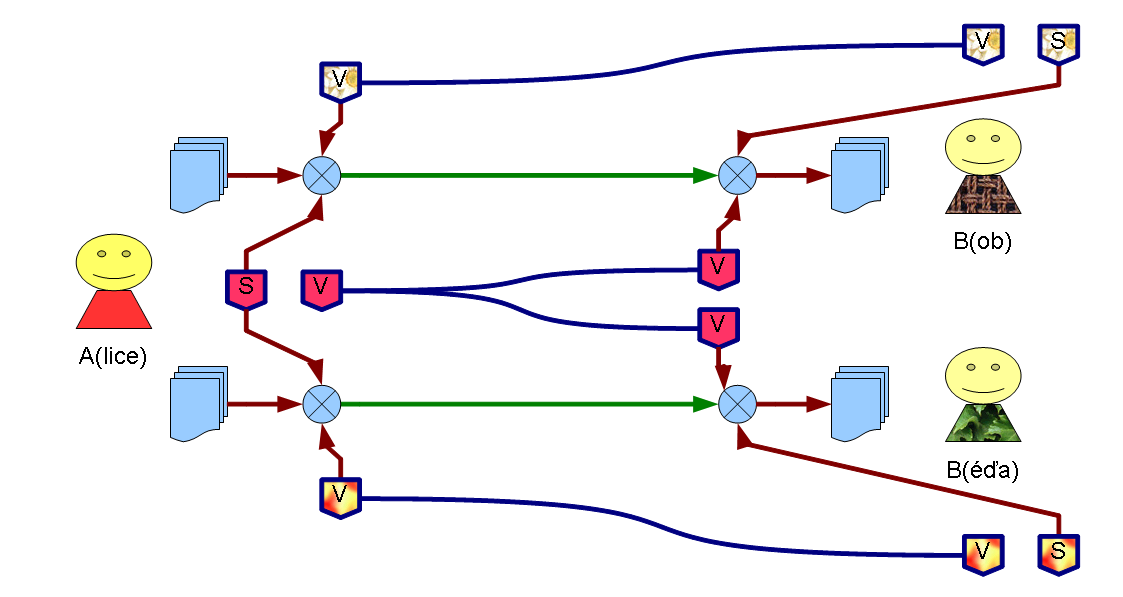
Zabezpečení proti přečtení zprávy a zároveň proti podvržení falešné zprávy

Sifr02-1 vice.png

Lze na takovou komunikaci vůbec zaútočit?

Všimněte si, že nám nevadí, když si útočník veřejné klíče přečte. Soukromé klíče, které musí zůstat tajné, se nikam nepředávají. To je veliká výhoda proti symetrickým šifrovacím metodám!


Běžné využití

TLS

Příklady šifrovacích algoritmů

Symetrické šifrovací algoritmy

DES
AES
Serpent
Twofish

Asymetrické šifrovací algoritmy

RSA


Zajímavost — historické šifry

Příklad: A h o j K a r l e + klíč 2 → C j q l M c t n g
Příklad: A h o j K a r l e + klíč 2 3 1 4 3 2 5 4 1 → C k p n M c w p f
Úkol
Vyzkoušejte si šifru Playfair

Chcete-li vyzkoušejte si šifrování šifrou Playfair. Zkuste zakódovat text: 

Šifruji jako blesk!

Pomocí klíče: 

Informatika

Řešení — výsledný šifrovaný text by měl znít: 

Looíl Rf, vnmg. Kmú gqbý.

(Interpunkce, diakritika a velikost písmen jsou přidány náhodně.)


Související stránky

Citováno z „http://mis.e-mis.cz/index.php/Princip_%C5%A1ifrov%C3%A1n%C3%AD“
Osobní nástroje
Jmenné prostory
Varianty
Akce
Výuka
Navigace
Nástroje