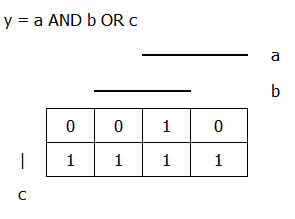Karnaughova mapa
Karnaughova mapa je jedním ze způsobů zápisu (logické) funkce.
Výhody Karnaughovy mapy:
- Ve srovnání se zápisem pomocí tabulky je úspornější (na velikost popsaného místa).
- Lze z ní jednoduchým způsobem získat zápis v disjunktivní nebo konjunktivní normální formě (DNF, CNF).
Obsah |
Princip
- Karnaughovu mapa je tabulka, kde každé kombinaci hodnot vstupních proměnných je přiřazena jedna buňka tabulky.
- Obsahem buňky je výsledek funkce při odpovídajícím ohodnocení vstupních proměnných.
- Buňky jsou uspořádány tak, že buňky se stejnou hodnotou některé proměnné jsou sousední buď přímo, nebo přes okraj tabulky.
Tedy pokud máme logickou funkcí dvou vstupních proměnných, nabývajících hodnot 0 nebo 1, pak Karnaughova mapa bude mít 4 buňky.
(Máme-li dvě proměnné a a b, pak mohou nabývat kombinací: 00, 01, 10 a 11.)
Příklady Karnaughových map
- Funkce jedné proměnné
Karnaughova mapa funkce NOT (funkce jedné proměnné):
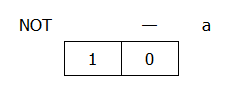
- pro:
a = 0tedy platíy = 1 - pro:
a = 1tedy platíy = 0
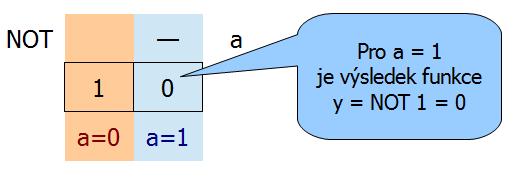
Přiřazení hodnot vstupních proměnných k buňkám Karnaughovy mapy funkce NOT:
- Funkce dvou proměnných
Karnaughova mapa funkce AND (dvě vstupní proměnné):
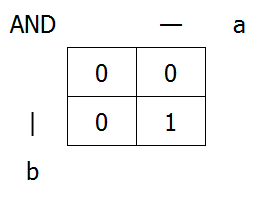
- pro:
a = 0ab = 0tedy platíy = 0 - pro:
a = 0ab = 1tedy platíy = 0 - pro:
a = 1ab = 0tedy platíy = 0 - pro:
a = 1ab = 1tedy platíy = 1
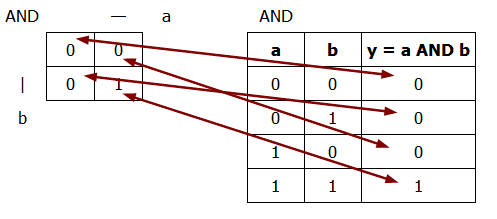
Přiřazení hodnot vstupních proměnných k buňkám Karnaughovy mapy funkce AND:
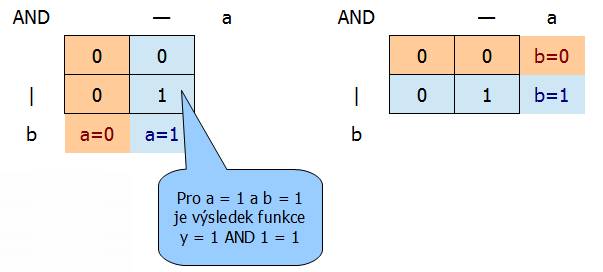
- Karnaughova mapa funkce tří proměnných
Přiřazení hodnot vstupních proměnných k buňkám Karnaughovy mapy funkce tří proměnných:

- Mapy funkcí více proměnných
Další mapy vzniknou podobným postupem tak, že se Karnaughova mapa funkce o k-1 proměnných jakoby „zrcadlově zkopíruje“ a spojením původní a „zkopírované“ části vznikne nová mapa funkce s k proměnnými.
Převod z mapy na tabulku
Převod z Karnaughovy mapy na tabulku je přímočarý.
- Mapa v každé buňce udává hodnotu funkce pro jednu kombinaci vstupních proměnných,
- stačí tedy přepsat čísla z mapy do správných řádků tabulky podle popisu mapy.