Konečný automat
(Vytvoření stránky) |
m (Přidán odkaz na stránku Regulární výrazy.) |
||
| Řádka 38: | Řádka 38: | ||
=== Poznámky: === | === Poznámky: === | ||
| − | # Konečné automaty jsou samozřejmě velmi základní, jednoduchý mechanismus, umožňující rozpoznávat pouze tzv. ''regulární jazyky''. Ale i tak jsou v matematice/informatice užitečné pro dokazování správnosti algoritmů, nebo lepší představu, jak algoritmy fungují. | + | # Konečné automaty jsou samozřejmě velmi základní, jednoduchý mechanismus, umožňující rozpoznávat pouze tzv. ''regulární jazyky'' (stejně jako třeba [[Regulární výrazy|regulární výrazy]]. Ale i tak jsou v matematice/informatice užitečné pro dokazování správnosti algoritmů, nebo lepší představu, jak algoritmy fungují. |
# Uvedené příklady jsou deterministické. NEDETERMINISTICKÝ konečný automat může mít pro jeden symbol více přechodů z jediného stavu. Takže třeba ze stavu q0 mohu při načtení písmene A přejít zároveň do stavů q4 a q6. Je to zjednodušení při návrhu, oba koncepty jsou stejně výpočetně silné, pro každý nedeterministický automat lze vyrobit deterministický takový, že přijímá stejný formální jazyk. ;) | # Uvedené příklady jsou deterministické. NEDETERMINISTICKÝ konečný automat může mít pro jeden symbol více přechodů z jediného stavu. Takže třeba ze stavu q0 mohu při načtení písmene A přejít zároveň do stavů q4 a q6. Je to zjednodušení při návrhu, oba koncepty jsou stejně výpočetně silné, pro každý nedeterministický automat lze vyrobit deterministický takový, že přijímá stejný formální jazyk. ;) | ||
| + | |||
| + | == Související stránky == | ||
| + | * [[Regulární výrazy]] | ||
Aktuální verze z 6. 12. 2017, 08:09
Konečný automat je abstraktní model výpočetního stroje (počítače/programu), který čte vstupní data (třeba posloupnost symbolů — třeba čísel či písmen) a na základě přečtených symbolů přechází z jednoho stavu do druhého.
Obsah |
Příklad
Z burzy mi přichází do počítače informace o poklesu nebo vzrůstu hodnoty akcií konkrétní firmy (třeba jednou za den). Je to zjednodušený příklad, takže předpokládejme, že přijde vždy jen informace (+) nebo (-) pro pokles nebo vzrůst. Chci, aby se mi rozsvítila kontrolka na monitoru, když nastal třikrát po sobě pokles.
Takovouto jednoduchou situaci umím namodelovat konečným automatem. V podstatě rozliším 4 stavy:
- Hodnota rostla, nebo jsem právě začal se sledováním.
- Hodnota poprvé klesala.
- Hodnota dvakrát po sobě klesala.
- Hodnota třikrát po sobě klesala – kontrolka svítí.
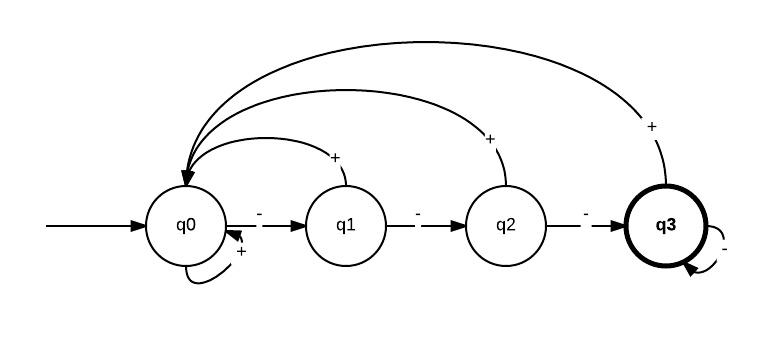
Budu mít tedy konečný automat se 4 stavy, označím si je q0,…, q3. Jeden stav je počáteční (stav q0). Koncový stav (kontrolka svítí, nastala hledaná situace) je stav q3. (Zakreslit to mohu jako 4 kolečka popsaná q0,…, q3, mezi nimi budu kreslit šipky přechodů mezi symboly.)
Tedy začínám v počátečním stavu q0. Dokud se objevuje (+) (růst), zůstávám v q0. (Lépe řečeno: přecházím znovu do q0, automat vždy do nějakého stavu přejde.) Jakmile přijde (-), přejdu do q1. Dalším (-) pokračuji do q2, (+) by mě vrátilo do q0. Atd. až se dostanu do stavu q3, který je konečný.
Automat tedy tzv. PŘIJÍMÁ formální jazyk nad abecedou ze dvou symbolů: {+, -}. Formální jazyk, který automat přijímá, je složen z posloupností, končících třemi a více symboly (-). (Pokud je automat v koncovém stavu, znamená to, že právě přečetl SLOVO, které patří do JAZYKA, který tento automat přijímá. ;)
Kreslení
Na kreslení můžeme použít třeba LucidChart.com.
Úkol
Zkuste si nakreslit konečný automat, který má jako abecedu písmena {a, b, c} a přijímá jazyk slov, která obsahují alespoň 3 písmena b (mohou být kdekoli ve slově a je jedno, kolik jakých jiných písmen ve slově je. Takže přijímá třeba slova:
- abaacbbac
- bbb
- baccbacaaab
- ccccbbccacb
- …
Poznámky:
- Konečné automaty jsou samozřejmě velmi základní, jednoduchý mechanismus, umožňující rozpoznávat pouze tzv. regulární jazyky (stejně jako třeba regulární výrazy. Ale i tak jsou v matematice/informatice užitečné pro dokazování správnosti algoritmů, nebo lepší představu, jak algoritmy fungují.
- Uvedené příklady jsou deterministické. NEDETERMINISTICKÝ konečný automat může mít pro jeden symbol více přechodů z jediného stavu. Takže třeba ze stavu q0 mohu při načtení písmene A přejít zároveň do stavů q4 a q6. Je to zjednodušení při návrhu, oba koncepty jsou stejně výpočetně silné, pro každý nedeterministický automat lze vyrobit deterministický takový, že přijímá stejný formální jazyk. ;)